Following their note on the issues that may arise from the ambiguity of EWS reservation policies, Aygün, Turhan, and Yenmez provide a critique of the multi-run deferred-acceptance algorithm currently used to implement de-reservation in the admission procedure of technical colleges. They outline three major limitations – the assignment of students to their less-preferred programmes, the potential disadvantage associated with reporting reserved category membership, and the scope for preference misreporting – and conclude by putting forth their own choice procedure for admissions to technical college programmes.
In the historic verdict of Ashoka Kumar Thakur vs. Union of India (2008), the Supreme Court of India granted 27% reservations to members of Other Backward Classes (OBC) in admissions to publicly funded higher educational programmes. In the same ruling, the Supreme Court explained what needs to be done if some OBC seats remain unfilled:
“27% is the upper limit for OBC reservation. The Government need not always provide the maximum limit. Reasonable cut off marks should be set so that standards of excellence are not greatly affected. The unfilled seats should revert to the general category.”
The Supreme Court, however, did not provide a well-defined procedure to revert unfilled OBC seats to the general category. The lack of specific guidance led to widespread ambiguity and numerous ad-hoc procedures, such as the one used in admissions to technical colleges.
Each year approximately 1.3 million students compete for 34,000 seats in technical universities in India. In 2015, a group of computer engineers and operations researchers collaborated with policymakers to change the admission procedure of technical colleges. One of the main design challenges was determining how de-reservations should be implemented.
Baswana et al. (2019a) report the new procedure, institutional details, and the interaction of the design team with policymakers.1 The new assignment procedure is based on iterated application of the celebrated deferred-acceptance (DA) algorithm of Gale and Shapley (1962) and called the ‘multi-run DA’.2 In the multi-run DA, the standard DA algorithm is first run with the initial category capacities at each university programme. If there are unfilled OBC seats at a programme, they are made open category seats by increasing the capacity of the open category and decreasing the capacity of OBC category at the programme. Then, the DA is re-run with all students and updated category capacities of programmes. The process is terminated when there are no unfilled OBC seats left in any programme.
How does the multi-run DA algorithm work?
We can explain the mechanics behind the multi-run DA with a simple example. Consider a programme that has eight seats, three of which are unreserved. One seat is set aside for Scheduled Castes (SC), one for Scheduled Tribes (ST), and three for OBC. There are eight students with the following merit score ranking
s1 − s2 − s3 − s4 − s5 − s6 − s7 − s8
Students s1, s2, s3, s7, and s8 are general category (GC) members, s4 is an OBC member, s5 is a member of SC, and s6 belongs to ST.
In the first iteration, three open category seats are assigned to s1, s2, and s3 because they have the highest merit scores. The SC seat is assigned to s5 and the ST seat to s6. Student s4 is assigned to one of the three OBC seats. At the end of this iteration, two of the three OBC seats remain empty. These two seats are reverted to the open category. Therefore, in the second iteration, the number of open category seats become five, and the number of OBC seats is reduced to one.
In the second iteration, the open-category seats are assigned to s1, s2, s3, s4, and s5 because they have the highest merit scores.3 Student s6 is assigned to the ST seat. The SC and OBC seats remain unfilled because s7 and s8 are GC students, and thus not eligible for these seats. The unfilled OBC seat is reverted to open category. Hence, in the third iteration, the number of open category seats increases to six and the number of OBC seats decreases to zero.
In the third iteration, the open category seats are assigned to s1, s2, s3, s4, s5, and s6 because they have the highest merit scores. Since s7 and s8 are GC students, the reserved SC and ST seats remain unfilled.
Shortcomings of the multi-run DA
At first glance, the multi-run DA mechanism seems promising and well thought out. But upon closer examination, critical issues with this mechanism can be identified. We highlight three main issues, emphasising the need for a better market design.
i) The first issue is that there is an unnecessary loss of student welfare because of the multi-run DA. To see this point, consider an example with programmes A and B with two seats each. At both programmes, one seat is open category, while the other one is reserved for OBCs. There are four students with the following merit score ranking: s1−s2−s3−s4. Students s1 and s2 are members of GC, while s3 and s4 are members of OBC. Students s1 and s2 prefer A over B, whereas s3 and s4 have the opposite preferences.
In the first iteration of DA, s1 and s2 apply to A, while s3 and s4 apply to B. Since s1 and s2 are both GC members, they are considered only for the open category seat. Therefore, at A, s1 is tentatively held for the open category seat and s2 is rejected. At B, s3 is tentatively held for the open category seat and s4 for the OBC seat. Next, the rejected student, s2, applies to the less-preferred programme B. Programme B tentatively holds s2 for the open category seat, s3 for the OBC seat, and rejects s4. Then, s4 applies to A and is held for the OBC seat, and s1 for the open category seat. The outcome is
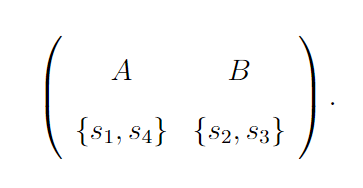
The first iteration of the multi-run DA is finalised because there is no unfilled OBC seat in any program. Note in this case that students s2 and s4 are assigned to their least preferred programmes.
When unfilled OBC seats are reverted in each programme’s choice procedure during the implementation of DA, all students can be assigned to their most-preferred programmes.4 In other words, a programme’s choice procedure is re-run when there are vacancies in the OBC category, with an updated number of seats for OBC and open category. In an update, the number of open category seats are increased and the number of OBC seats are decreased. In the example above, when s1 and s2 apply to A, s1 is assigned an open category seat and the OBC seat remains vacant. Since there is an unfilled OBC seat, OBC and open category capacities are updated so that open category has two seats, while there is no OBC seat left. Under the updated capacities, both s1 and s2 are assigned to A. The outcome is
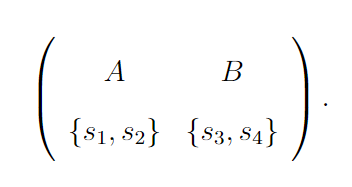
In this scenario, both s2 and s4 are assigned to a more-preferred programme using this alternative mechanism, while reservation policies are still implemented.
ii) The second issue is that reporting the reserved category membership may be detrimental to students belonging to these categories, who are the purported beneficiaries of vertical reservations. To see this, suppose that s4 does not report her OBC membership in the same example.5
In the first iteration of multi-run DA, s1 and s2 apply to A, while s3 and s4 apply to B. Programme A tentatively holds s1 for the open category seat and rejects s2. Programme B tentatively holds s3 for the open category seat and rejects s4, because s4 did not declare her OBC membership. Next s2 applies to B and s4 applies to A. In B, s2 receives the open category seat by replacing s3, and s3 receives the OBC seat. In A, s1 keeps her open category seat and s4 is rejected. Therefore, the outcome of the first DA iteration is
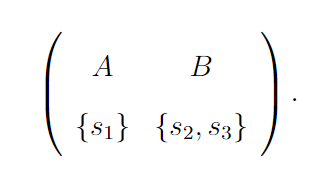
Meanwhile the OBC seat in A remains unfilled, and it is reverted to open category. Hence, both seats in A are now open category. The DA algorithm is run again with the updated capacities. Students s1 and s2 apply to A, and they are both assigned to an open category seat because A has two open category seats. Students s3 and s4 apply to B. Student s3 is assigned to the open category seat and s4 gets rejected. Next the rejected student s4 applies to B. However, she gets rejected because her merit score is lower than both s1 and s2. Therefore, the second iteration of DA produces
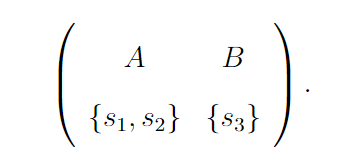
Since the OBC seat in B is empty, it is reverted to an open category seat. Therefore, B also has two open category seats now. In the third iteration, both programmes have two open category seats. Students s1 and s2 apply to A and they are both assigned to an open category seat. Students s3 and s4 apply to B and they are both assigned to an open category seat as well. Therefore, the outcome of the third DA iteration is
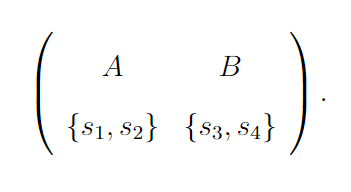
Since there is no unfilled OBC seat, the multi-run DA terminates and assigns students to programmes according to the matching above. Note that when s4 truthfully reveals her OBC category membership she was assigned to A, which is her second choice. However, when she does not reveal her membership, she is assigned to her top choice – programme B.
This example shows that it is possible for a reserved category member to get assigned to a less preferred programme if she declares her reserved caste status. This is fundamentally against the spirit of reservation policies.
iii) The third issue is that the multi-run DA is vulnerable to manipulation by preference misreporting. In the example above, s2 is assigned to B. Student s2 can misreport her preference ranking and obtain the more preferred programme A. Suppose that she lists A as the only acceptable programme in her preference ranking. The outcome of the multi-run DA becomes
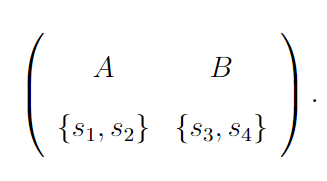
Therefore, s2 is assigned to A by misreporting her preference ranking, whereas she is assigned to B when she reports her preference ranking truthfully. Since s2 prefers A to B, she receives a more preferred programme by misreporting her preferences.
Proposed solution: how market designers can help
Starting with Hafalir et al. (2013) and Ehlers et al. (2014), researchers in market design have studied the use of reservation systems in allocating scarce resources. Hafalir et al. (2013) and Echenique and Yenmez (2015) paved the way to reconcile reservation systems with the celebrated DA mechanism put forth by Gale and Shapley, by carefully designing programmes’ selection procedures and embedding them into the DA.
Following their tradition, we designed a choice procedure for Indian college programmes to implement the comprehensive reservation policies (Aygün and Turhan 2022b). We introduced a selection criterion for the programmes – the ‘backward transfers choice’ rule – by jointly taking reservations and de-reservations into account. We showed that the DA algorithm, coupled with the backward transfers choice procedure, solves the issues that come up when using the multi-run DA. Moreover, we showed that the DA algorithm with backward transfer choice rule is the only mechanism that satisfies the reservation policies.
The multi-run DA mechanism iteratively runs the DA mechanism on all candidates repeatedly to handle de-reservations. In our proposed solution, the DA algorithm is run only once because de-reservations are disentangled using the programmes’ choice rules. In other words, while the multi-run DA re-runs the whole DA algorithm, we propose re-running programmes’ choice rules to handle de-reservations. This seemingly straightforward and small change increases students’ welfare (possibly significantly), and removes all strategic manipulation possibilities. The findings show that students receive more-preferred assignments under this procedure compared to the multi-run DA outcome.
An important design concern for our backward transfers choice rule is setting higher cut-off scores for open category than reserved categories. There may be other design objectives – selecting the most meritorious set of students subject to the legally mandated reservation policies would be one such desideratum. In Aygün and Turhan (2022a), we designed a selection procedure – the ‘forward transfer choice’ rule – to achieve this objective. In a forward transfer choice rule, the open category is filled first following applicants’ merit scores. Then, reserved category seats are filled following merit scores. If some OBC seats remain unfilled, then they are made open category seats, and filled with the remaining applicants based on merit scores. Therefore, the processing order of categories in a forward transfer rule ends with an open category when there are vacancies in the OBC category.
Among the de-reservation policies that satisfy the over and above principle, the forward transfer choice rule is the one that selects the most meritorious set of students, and fills vacant OBC positions at the end of the processing sequence by only considering the remaining applicants. Conversely, the backward transfer rule fills the vacant OBC positions by considering all applicants at the beginning of the processing order, whereas the forward transfer choice rule, thus ensuring higher cut-off scores for open category than reserved categories, whereas the forward transfer rule selects a more meritorious set of students.
This post is the third in a three-part series on 'The architecture of affirmative action'.
Notes:
- Their design is a joint seat allocation process for Indian Institutes of Technology (IITs) and non-IITs. The algorithmic details can be found in Baswana et al. (2019b).
- The DA algorithm was proposed by Gale and Shapley (1962) to find a stable matching between men and women, or students and colleges.
- Note that the OBC student s4 and the SC student s5 are both assigned to open category seats.
- See Aygün and Turhan (2022b) for more details.
- It is optional for students to report their category membership.
Further Reading
- Aygün, O and B Turhan¨ (2022a), ‘Affirmative action in India: Restricted strategy space, complex constraints, and direct mechanism design’, Iowa State University Working Paper.
- Aygün, Orhan and Bertan Turhan¨ (2022b), “How to de-reserve reserves: Admissions to technical colleges in India”, Management Science, forthcoming.
- Baswana, Surendra, Partha Pratim Chakrabarti, Sharat Chandran, Yashodhan Kanoria and Utkarsh Patange (2019a), “Centralized admissions for engineering colleges in India”, INFORMS Journal on Applied Analytics, 49(5): 338-354.
- Baswana, S, PP Chakrabarti, S Chandran, Y Kanoria and U Patange (2019b), ‘Joint Seat Allocation 2018: An algorithmic perspective’, arXiv Technical Report.
- Echenique, Federico and M. Bumin Yenmez (2015), “How to control controlled school choice”, American Economic Review, 105(8): 2679-2694.
- Ehlers, Lars, Isa E Hafalir, M. Bumin Yenmez, and Muhammed A Yildirim (2014), “School choice with controlled choice constraints: Hard bounds versus soft bounds”, Journal of Economic Theory, 153: 648-683.
- Gale, David and Lloyd Shapley (1962), “College Admissions and the Stability of Marriage”, American Mathematical Monthly, 9(1): 9-15.
- Hafalir, Isa E, M. Bumin Yenmez and Muhammed A Yildirim (2013), “Effective affirmative action in school choice”, Theoretical Economics, 8(2): 325-363.




 16 December, 2022
16 December, 2022 





Comments will be held for moderation. Your contact information will not be made public.