The Economic Survey 2018-19 highlights that the single biggest constraint to the ease of doing business in India is contract enforcement and dispute resolution, and that increasing capacity in lower judiciary is crucial. This article estimates that adding one judge to a court with vacancy increases bank lending by 0.5% a year later, which affects credit availability, production, and profitability of firms located within the court’s jurisdiction.

Most civics textbooks in Indian middle schools present the judiciary as one of the three key pillars of a democracy. From a governance sense, the judiciary upholds the values enshrined in a constitution and is supposed to act as a check against executive and legislative powers. However, its role extends far beyond this definition, by instilling a sense of trust in markets and the functioning of the economy. In particular, courts enforce contracts and promote de facto rights, which enable individuals and firms to efficiently allocate resources to improve welfare. However, timely enforcement is essential to reduce uncertainties and transaction costs that likely have both efficiency- and equity-related consequences. A cross-country correlation between GDP (gross domestic product) per capita and trial duration (Figure 1) depicts a negative association. Does this also mean that slow trials cause lower growth? In recent research (Rao 2019), I analyse the causal relationship between the performance of district courts, local bank lending operations locally, and formal sector firm outcomes in India.

Figure 1. Cross-country correlation between GDP per capita and trial duration

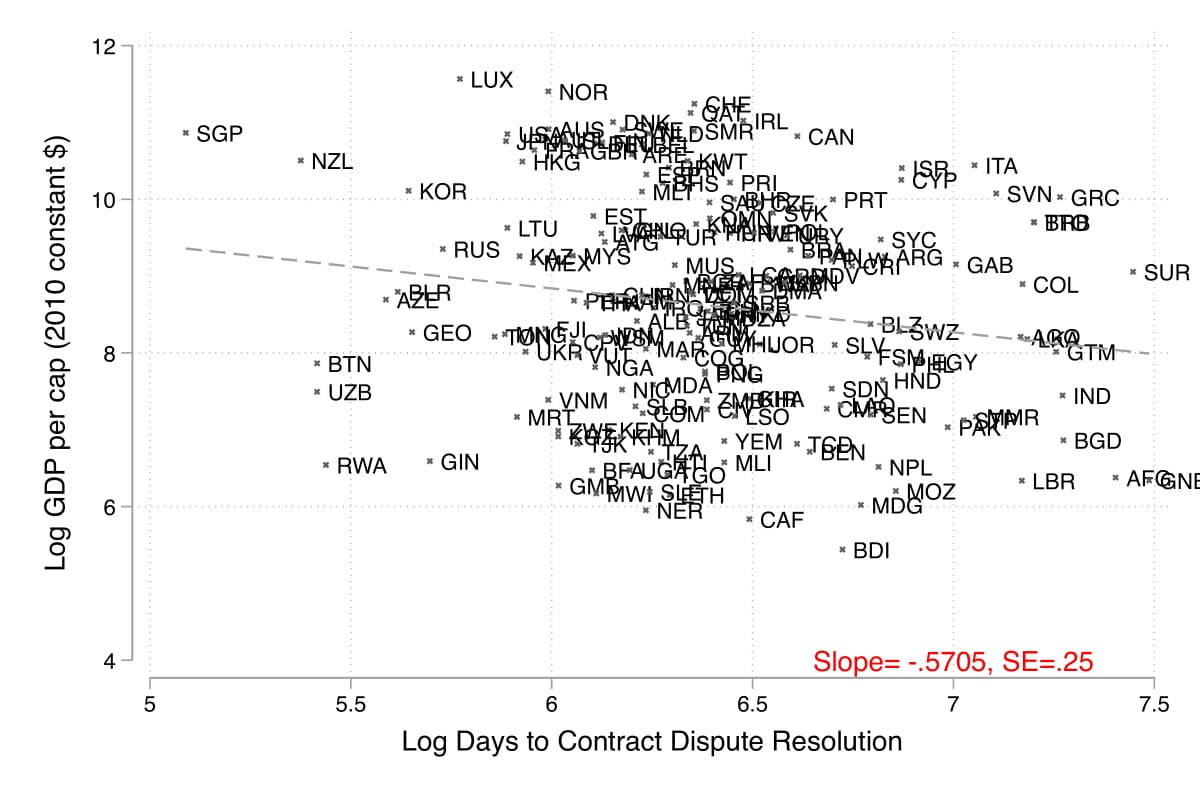
Data source: Cross-country time-series data (2004-2018) from the World Bank’s Doing Business (Trial Duration) and World Development Indicators (GDP).

Note: The negative slope of -0.57 implies that a 1% increase in trial duration is associated with a 0.57% decrease in GDP per capita. Standard Error of 0.25 implies that the estimate of the slope is statistically different from 0, and the association is statistically significant with 95% confidence.

The Indian case

In India, the average per capita backlog of trials in district courts is 10 times larger than similar courts in the US. This probably does not come across as a surprise to many in India, given the regular coverage by the media of court delays and large pendency. I examine the causal effects of backlog in district courts due to high levels of judge vacancy on three key economic outcomes. First, I analyse the role of these backlogs on contract enforcement in the local credit markets through bank lending behaviour. Second, I explore how this affects credit availability for formal-sector firms, and subsequently, their production and profitability. Third, I estimate the benefit-to-cost ratio of reducing backlog by adding more judges to courts. The results indicate that adding one more judge increases bank lending by 0.5% over a baseline level of 350,000 loans per district. This increases averageF firm profits by 1.6% or US$ 750 per judge, yielding an 8:1 benefit-to-cost ratio to the public purse.

The data

I assembled a novel dataset on the universe of 6 million court cases active between 2010 and 2018 across 195 district courts in India, merged with panel data on formal sector firms¹. The granularity of the data allows me to construct a measure of court performance that I call the disposal rate, reflecting the timeliness of the adjudication process. This indicator is the ratio between the number of trials resolved in a given year and the total caseload, expressed in percentage terms. An important factor affecting court performance is judge vacancy, that is, the percentage of judge posts in a court that are vacant. Courts in my sample have an average of 18 judge posts, of which 23% are vacant.²

Litigation patterns among firms

Data on firms matched to trials indicate that banks are primary users of district courts, where they appear as petitioners in over 80% of trials involving them. Specifically, close to 50% of all banks in the firm sample find a match in the trial dataset. In contrast, the match rate is much lower at 13% for non-financial firms. Encoding a random sample of judgements in trials involving banks indicate that about two-thirds of them are related to debt recovery. Though there are specialised tribunals such as the Debt Recovery Tribunal to adjudicate debt-specific disputes over a certain monetary threshold, district civil courts are frequently the adjudicator in the instances of ordinary debt disputes. Typical examples of such litigation include non-repayment of housing or education loans by individuals as well as small loans taken by firms. Heavy backlog in courts imply that all this capital lent remains stuck, potentially adding to the mounting non-performing assets of the lender bank.

Figure 2. Litigation intensity across firms

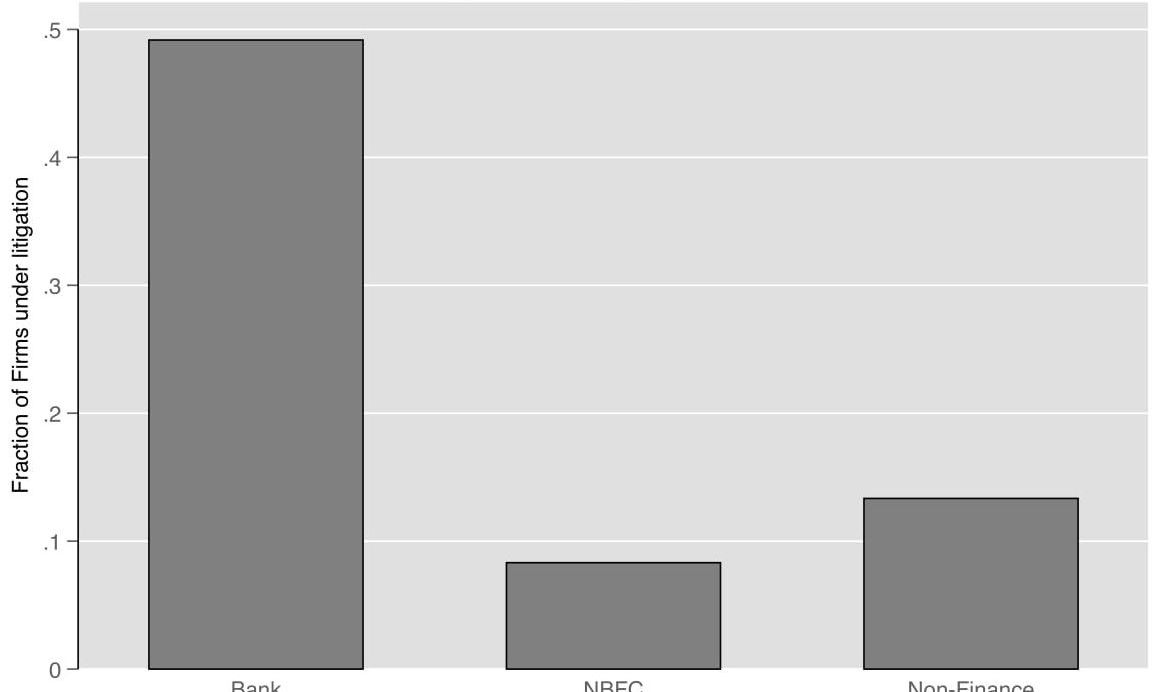
Note: The y-axis presents the fraction of firms by sector in Prowess dataset that are engaged in a trial in the court sample. NBFC refers to non-banking financial companies.

Empirical strategy

Annual variations in court backlog, trial resolutions, and filings are likely correlated with unobserved district-specific time-varying characteristics such as migration flows, changing district policy climate, or varying levels of crime that are likely to affect both court performance as well as lending and firm outcomes. Additionally, there is also concern of reverse causality, where court performance could be lower in places with increasing trends in economic and firm-specific outcomes. For example, locations on a higher firm growth trajectory, such as fast growing cities, may mechanically lead to more litigation in their corresponding district court, adding to backlog.

To address this, I take advantage of features of the Indian judiciary that allows me to exploit as good as random variation in judge vacancy within a district court to account for unobserved factors driving the possible correlations between court performance and outcome measures. Specifically, this variation arises from a judge rotation policy that shifts existing vacancies over time. Judge rotation is handled centrally at the level of each state high court that fixes judges’ tenure to a relatively short period due to the sensitivity of the position. Judges are never assigned districts that are their hometowns or where they have any sort of legal experience. This policy is similar across all Indian states, with minor variations.³ Since judges are central to the functioning of courts, any increase or decrease in judge vacancy strongly affects court performance.

I estimate the causal relationship in two stages.⁴ The first stage examines the relationship between judge vacancy and court performance. The second stage estimates the causal relationship between court performance as predicted by judge vacancy, and outcome measures. The first stage relationship is strong, indicating that a one percentage point increase in judge occupancy (100 – judge vacancy) increases overall disposal rate by 1%.

Figure 3. Relationship between court performance and judge occupancy

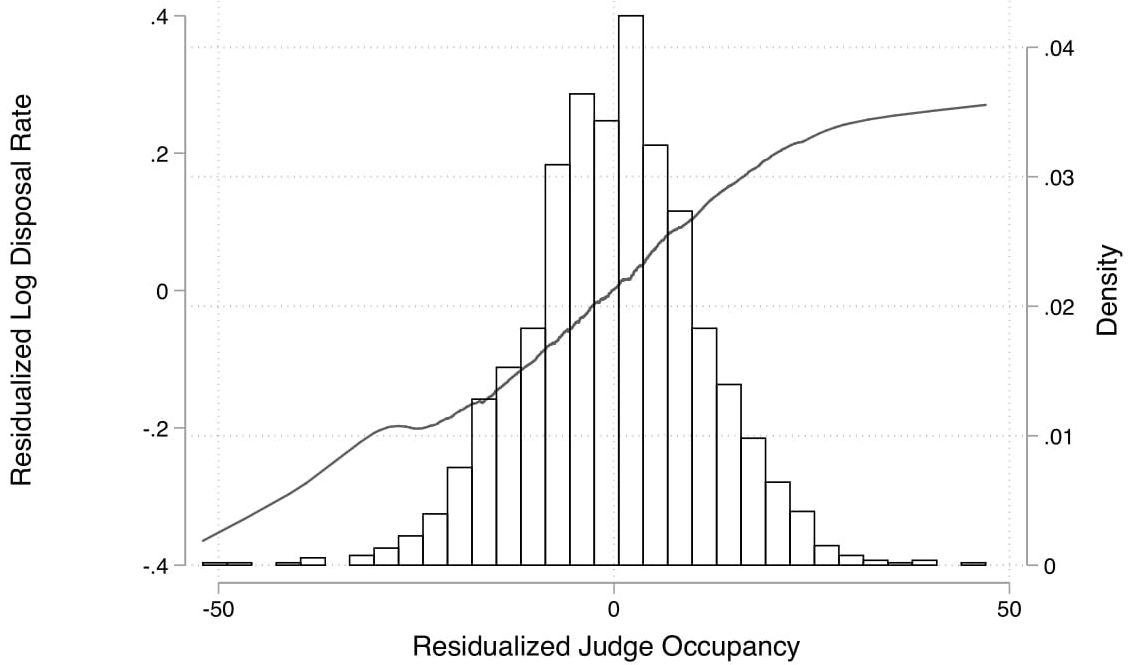
Note: The x-axis and y-axis represents de-meaned judge occupancy (100-judge vacancy) and disposal rate respectively. Therefore, these are centred around 0, which represents their respective mean or average values.

Effects on lending behaviour

The effects on banks capture the direct impact of courts through the litigation process. Since banks are intensive users of courts, improved court performance should enable timely enforcement of credit contracts and affect subsequent lending behaviour. Consistent with this hypothesis, using district-level credit summary data by the Reserve Bank of India (RBI), I find that a 1% increase in disposal rate increases the total number of loans by 0.11% one year later or that adding one more judge to a court with vacancy increases lending by 0.5%. This is large considering that banks have an average of 350,000 loan accounts per district.

An examination by the type of bank shows that this increase is even larger for public sector banks, which represent close to 80% of all banks in the country. Further, I find that loans towards manufacturing and consumption experience a significant increase, suggesting that courts are important in the functioning of credit markets, which stimulate production and consumption in an economy.

Figure 4a. Effect of increase in court disposal rate on bank lending

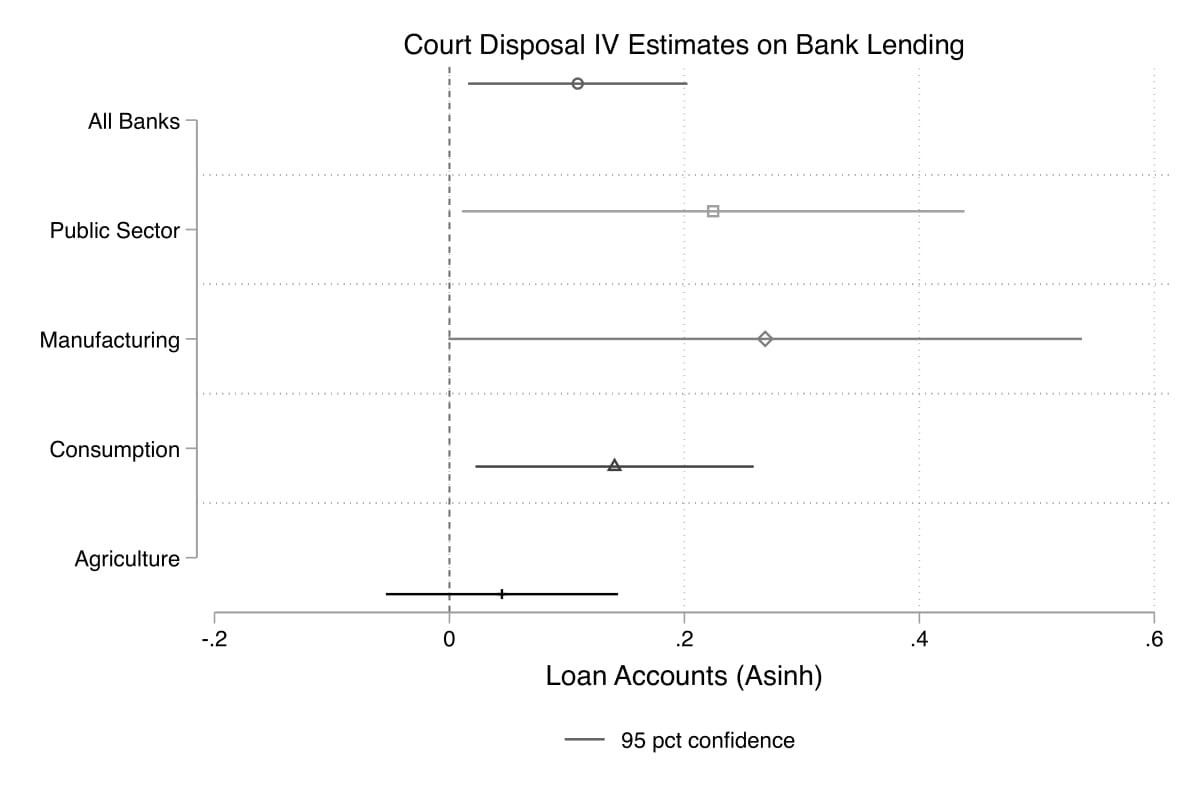
Figure 4b. Effect of increase in court disposal rate on firms’ borrowing from banks

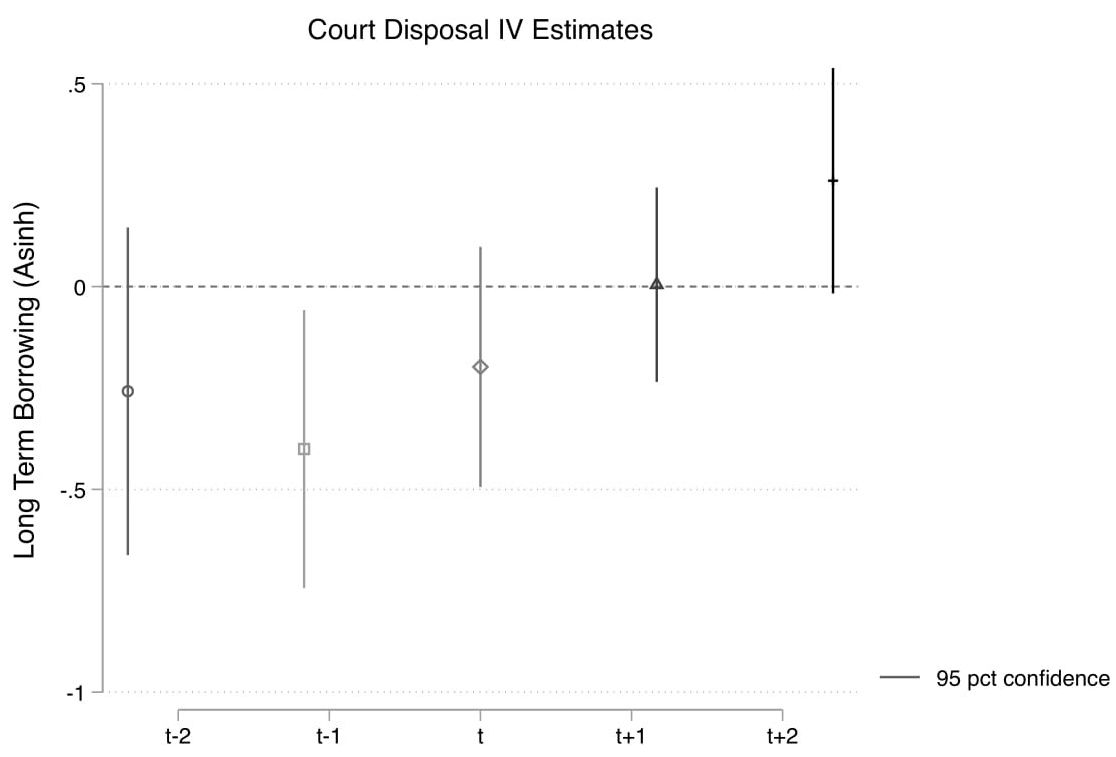
Note: The graphs represent the causal relationship between court disposal rate and outcome measures. 4a depicts this relationship with respect to the number of loan accounts in a given district across all Scheduled Commercial Banks. 4b shows the relationship with respect to firms’ loan amount borrowed from banks. The x-axis in 4b presents the time horizon. This shows that an improvement in court disposal rate in a given year (t) affects the extent of borrowing two years later (t+2). All outcome measures have been transformed such that the estimates can be interpreted in terms of percentage changes when disposal rate increases by 1%. The error bars around the estimates represent a 95% confidence interval: that is, there is a 95% probability that the estimate lies within this range.

Effects on firm production

Next, I examine the effects on all firms with registered office inside the territorial jurisdiction of my sample courts. On the firms’ side, I find an increase in long-term borrowing (with repayment beginning one year from borrowing) from banks (Figure 4b). Borrowing from banks increases on average across all firms, and particularly among those firms with ex-ante assets size below the median. On the other hand, there is no change in bank borrowing among firms with ex-ante assets above the median. As a result of improved credit availability, firm production improves. I find that a 1% increase in disposal rate increases wage expenditure by 0.2%, sales revenue by 0.11%, and profits by 0.26% on average, two years later. Figure 5 below illustrates this relationship two years before and two years after an increase in disposal rate.

Figure 5. Effect of increase in court disposal rate on wage bill, sales revenue, and profits of firms

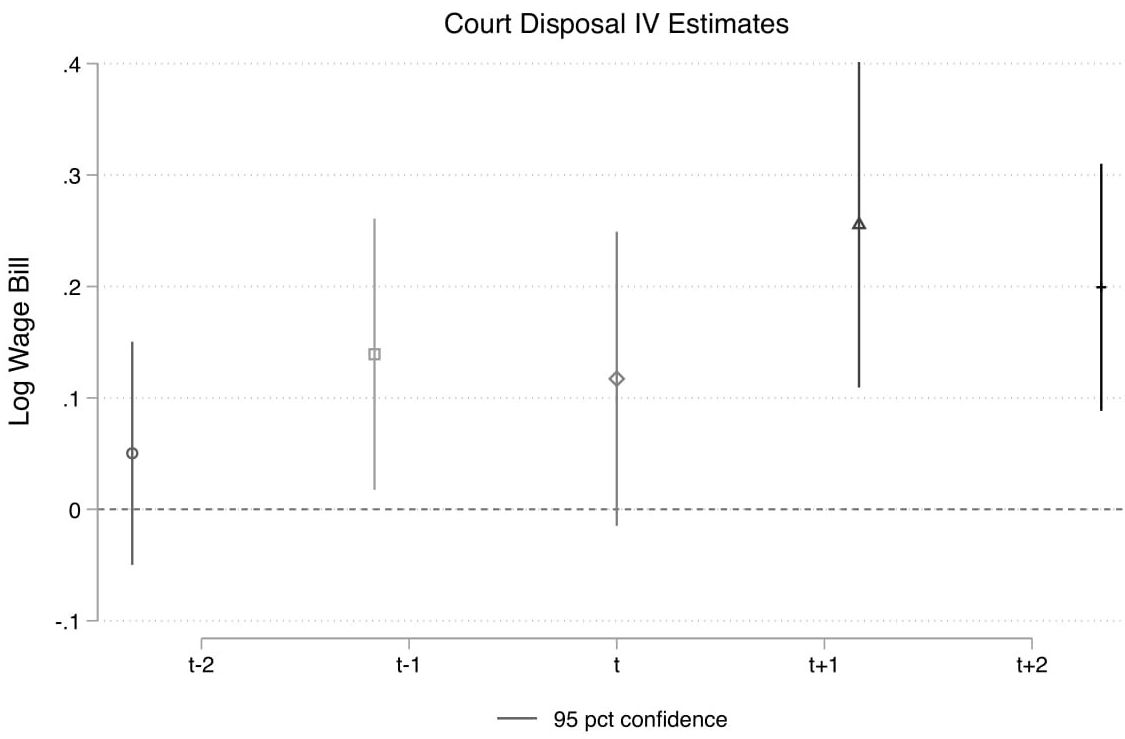
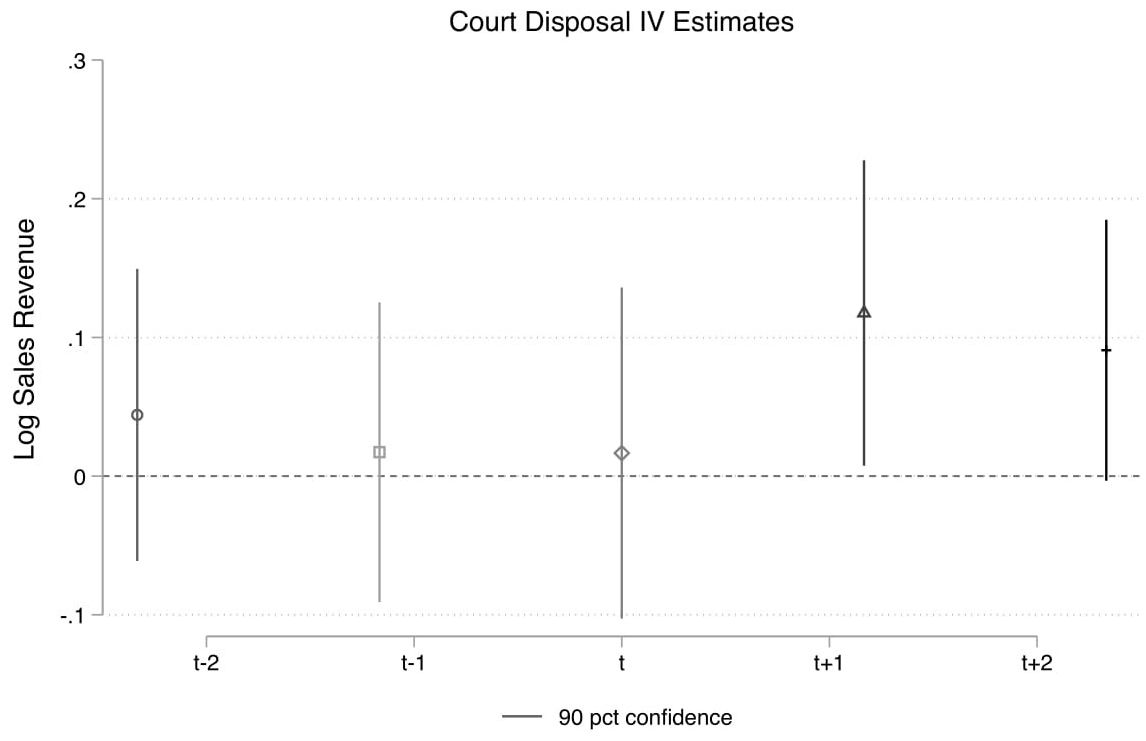
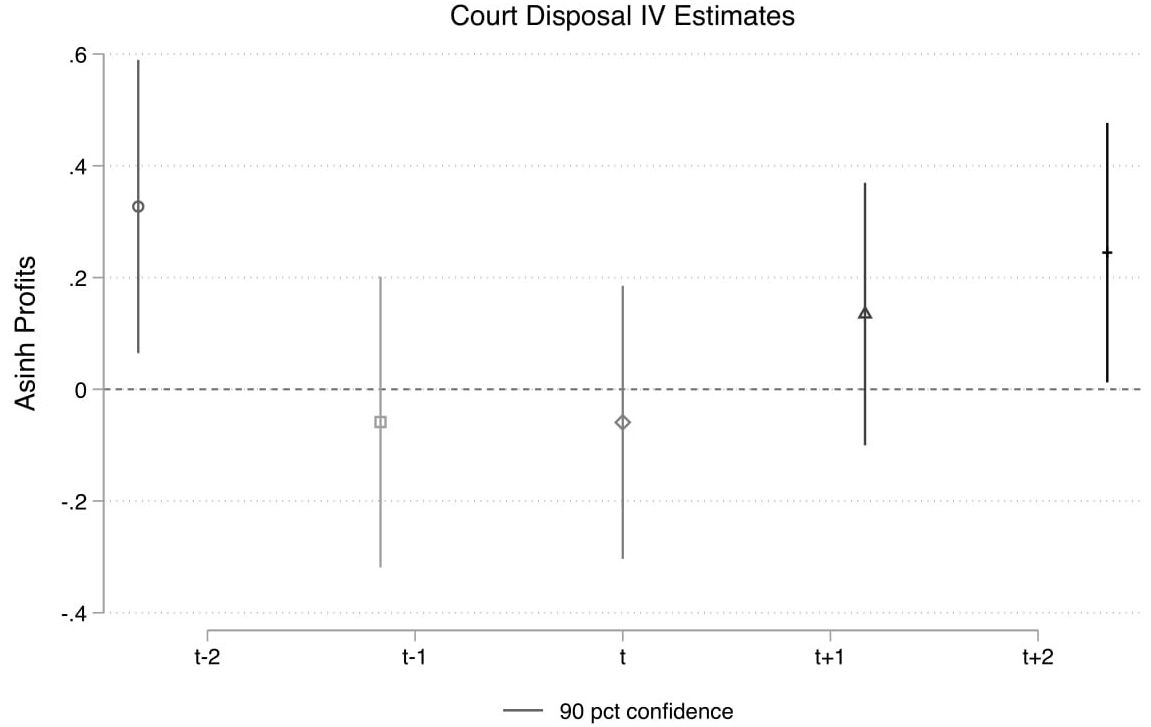
Note: The x-axis presents the time horizon. This shows that an improvement in court disposal rate in a given year (t) affects the outcomes one-two years later. All outcome measures have been transformed so that the estimates can be interpreted in terms of percentage changes when disposal rate increases by 1%. The error bars around the estimates represent a 95% confidence interval, that is, there is a 95% probability that this estimate lies within this range.

Policy implications

Adding one more judge to a district court with vacancy increases disposal rate by 6%. This translates to an increase in profits of about Rs. 53,000 per firm, which is a 1.6% increase over a baseline median profit of Rs. 3.3 million. With about 800 formal-sector firms per district and a value added tax rate of 18% on basic manufacturing and services, the state could potentially earn close to Rs. 7.6 million in taxes in the short run from each district. On the other hand, the average annual salary of a district judge is under Rs. 1 million. Thus, reducing judge vacancy has an implied benefit-cost ratio of approximately 8:1 with respect to tax revenue. Given that the annual budgetary outlay for the law and justice sector is less than a tenth of a percent of the total 2019 expenditures, there is a justifiable reason for increasing public expenditure to address the problem of vacancies in the district judiciary.

Notes:

1. For firms, I use the Prowess dataset compiled by the Centre for Monitoring the Indian Economy (CMIE).
2. Average disposal rate is 14%, with a standard deviation of 12%. The average trial duration of a case at the time of disposal is 617 days with a standard deviation of nearly 500 days. Standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of values from the mean value (average) of that set.
3. I account for any state-specific time-varying differences by including state-year fixed effects. Additionally, I account for any time-invariant district-specific unobserved characteristics by including district fixed effects. What this means is that my statistical models only use within-district variation in court variables and outcome measures.
4. The statistical model is known as Two-Stage Least Squares Estimation that operationalises the Instrumental Variables (IV) design. IV design is a technique for causal inference that is based on exploiting as good as random variation in the explanatory variable so that the resulting correlation with the outcome/dependent variable can be construed as causal.

Further Reading

• Rao, M (2019), ‘Judges, Lenders, and the Bottom Line: Court-ing Firm Growth in India’, Job Market Paper.
• Kondylis, F and M Stein (2018), ‘Reforming the Speed of Justice: Evidence from an Event Studyin Senegal’, The World Bank Working Paper Series, page 65.
• Boehm, J and E Oberfield (2018), ‘Misallocation in the Market for Inputs: Enforcement and the Organization of Production’, Technical Report dp1572, Centre for Economic Performance, London School of Economics and Political Science, London, UK.
• Ponticelli, Jocopo and Leonardo S Alencar (2016), “Court Enforcement, Bank Loans, and Firm Investment: Ev-idence from a Bankruptcy Reform in Brazil”, The Quarterly Journal of Economics, 131(3):1365-1413.
• Visaria, Sujata (2009), “Legal reform and loan repayment: The microeconomic impact of debt recovery tribunals in India”, American Economic Journal: Applied Economics, 1(3):59-81.